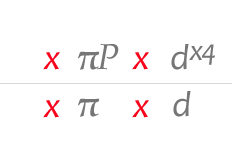He dreamt he was challenged by a Woman (always a woman) to find a way to calculate the surface area of a nine-inch (?) circle without making use of pi.
As you well know the number π is a mathematical constant that is the ratio of a circle's circumference to its diameter, and is approximately equal to 3.14159. It has been represented by the Greek letter "π" since the mid-18th century, though it is also sometimes written as pi. π is an irrational number, which means that it cannot be expressed exactly as a ratio of two integers (such as 22/7 or other fractions that are commonly used to approximate π)
For thousands of years, mathematicians have attempted to extend their understanding of π, sometimes by computing its value to a high degree of accuracy. Before the 15th century, mathematicians such as Archimedes and Liu Hui used geometrical techniques, based on polygons, to estimate the value of π. Starting around the 15th century, new algorithms based on infinite series revolutionized the computation of π, and were used by mathematicians including Madhava of Sangamagrama, Isaac Newton, Leonhard Euler, Carl Friedrich Gauss, and Srinivasa Ramanujan.
Enough WIKI; back to bed.
The Dreamer loved a challenge. Particularly one that pitted him against the Giants of Geometry and the Masters of Math.
With a toss and a turn, he pondered, and in way way way less time than you've taken to read this sentence, he figured it out—EUREKA!—a simple and stately solution. The Woman acted less-than-whelmed.
Upon rising, The Dreamer put in train the process that would prove his heretofore undreamt-of method for calculating the surface area of a circle. At the same time he thought he might as well throw in an equation for figuring its circumference as well.
To test his breakthrough theory, The Dreamer first needed to create a perfectly circular disk with a 9-inch diameter that was precisely one-inch thick.

Unfortunately, to truly prove the theory, the disk had to be made of 24-carat gold. Costly, but necessary. The disk had to be carefully cast and precisely machined to extremely close tolerances—with crisp, sharp-cut edges. In less time than it's taken you to read this paragraph; it was done. And beautiful to see.
The disk—it was quite heavy—needed to be weighed. The scale of choice: the A&D GX-10K industrial balance—with accuracy to three ten-thousandths of an ounce (0.00035274).
As shown in figure 1, the disk weighed in at 647.5512 ounces (troy). A big boy!
The rest―simplicity.
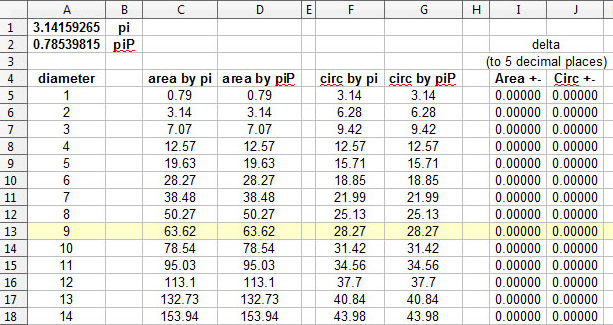
Calculate the weight of a 9-inch by one-inch thick SQUARE of solid, pure gold. The calculation looks like this: [(9-inches * 9-inches * 1-inch) * 10.17886 (which is the weight in ounces of one cubic inch of gold)]. This calculation runs out to 824.48776 troy ounces for the nine-by-nine-by-one-inch square.
Then divide the weight of the disk by the weight of the square and you have the New Pi (called piP): 0.78539815.
Et sic sequitur . . .
The area of any circle will be 78.539815% of the area of a square where the diameter of the circle equals the side of the square.
Similarly, the circumference of a circle will be 78.539815% of the perimeter of a square where the sides of that square equal the diameter of the circle.
The New Geometry (based on a 9-inch circle): area—[pi * radius-squared]: 3.14159265 * (4.5 * 4.5) = 63.61725 circumference—[pi * diameter]: 3.14159265 * 9 = 28.27433
The New Geometry:
area—[piP * diameter-squared]: 0.78539815 * (9 * 9) = 63.61725
circumference—[piP * (diameter * 4)]: 0.78539815 * (9 * 4) = 28.27433
The proofs: Do your own comparisons: Enter a diameter in the box on the left then click the “=” button. And so, Astounded Reader, nothing for it now but to contact your local Nobel Prize Committee with the obvious recommendation that The Dreamer be put on the (very!) short list for the 2021 Prize in Physics and HTML Perseverance.
This the link you will need. Tarry not!
Area of a Circle
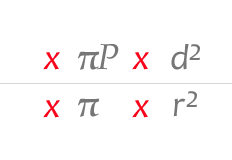

Circumfrence of a Circle